Fisherの直接確率法

Fisherの直接確率法（フィッシャーの直接確率法）

カイ二乗検定より正確な確率を求める方法。計算量が多いため、昔は多く使われていなかった。

カイ二乗検定にもカイ二乗検定/Yatesの補正という方法があるが、それよりもFisherの直接確率法の方が正確。

実測値の表

期待値の表

記号の表

これからa=0となる場合の確率P(a=0)を計算してみる。

まず、R1とR2がそれぞれ6, 6になる確率P(R0)を求める。期待値の表をみると、暴露ありの確率は、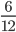 $\frac{6}{12}$ 暴露なしの確率は、 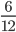$\frac{6}{12}$ なので、、12人を選んだときそれぞれ6人ずつになる確率は以下のようにして求められる。

$P(R _0) = _{12} C _6 \times (\frac{6}{12})^6 \times (\frac{6}{12})^6$

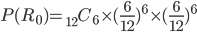
C1とC2がそれぞれ4, 8になる確率をP(C0)とすると、 $P(C _0) = _{12} C _4 \times (\frac{4}{12})^4 \times (\frac{8}{12})^8$

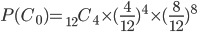
実測値の値、4,2,0,6になる確率をP(M0)とすると、

$P(M _0) = \frac{12!}{4! 2! 0! 6!} (\frac{4}{12})^4 \times (\frac{2}{12})^2 \times (\frac{0}{12})^0 \times (\frac{6}{12})^6$

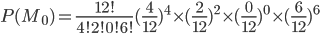
実測値が出現する確率は、行と列の合計がR, Cとなる場合の中で、a,b,c,dが4,2,0,6となる確率なので、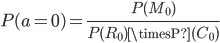 $P(a=0) = \frac{P(M _0)}{P(R _0) \times P(C_0)}$ となる。

実際に計算するとP(a=0) = 0.00303となる。

同様にP(a=1, 2, 3, 4)についても計算してみる。

P(a=0) = 0.0303
P(a=1) = 0.2424
P(a=2) = 0.4545
P(a=3) = 0.2424
P(a=4) = 0.0303

a=2となる場合が期待値の通りであり、P値は1となる。ここから外れるほど、P値は低くなる。

a=0なる場合とa=4となる場合は、片側検定ではP値は0.0303となるが、両側検定であれば、a=0とa=4の2つの確率を足した0.0606がP値となる。

a=1またはa=3となる場合は、それよりも偏った場合の確率を足して、片側検定では、0.2424+0.0303=0.2727となり、両側検定では0.5454となる。