重回帰分析/決定係数
重回帰分析において、目的変数が説明変数によってどのぐらい説明できているかの目安。
決定係数は0から1までの値をとり高いほどよい。
決定係数が0.5ということは、目的変数の分散の50%が説明変数によって説明できるということを表している。
決定係数とは、重回帰式で予測される値の分散÷目的変数の分散であり、重回帰式で予測される値と目的変数の値の相関係数の二乗でもあり、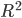 と表記される(
と表記される(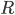 は相関係数)
は相関係数)
計算方法
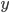 を目的変数、
を目的変数、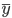 を目的変数の平均値、
を目的変数の平均値、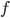 を重回帰式による目的変数の予測値、
を重回帰式による目的変数の予測値、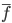 をその平均値とすると、
をその平均値とすると、
決定係数 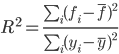 である。
である。
誤差の分散で計算する場合
(目的変数の分散) = (重回帰式で予測される値の分散) + (誤差の分散) なので、
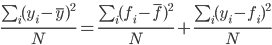
であり、
決定係数 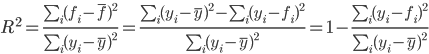 ともかける。
ともかける。
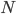 をサンプルサイズとし、以下のように考えると、
をサンプルサイズとし、以下のように考えると、
誤差の分散 = 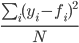
目的変数の分散 = 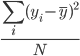
決定係数 = 1 - 誤差の分散/目的変数の分散 ともいえる。
自由度調整済み決定係数
説明変数の数が異なると、決定係数の大小を比べることができないので、説明変数の数で調整した決定係数のこと。
変数選択を行う際、どの変数の組み合わせがよいか検討する際、適合度の指標として使える。
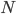 をサンプルサイズ、
をサンプルサイズ、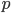 を説明変数の数とすると、
を説明変数の数とすると、
自由度調整済み決定係数 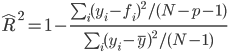 となる。
となる。
これは誤差の二乗、目的変数の偏差の二乗をそれぞれの自由度で割った値であり、それぞれ誤差と目的変数の不偏分散と考えることができる。つまり、母集団を想定した場合の決定係数と考えることができる(要確認)。
決定係数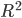 を用いて、
を用いて、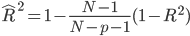 とする本もあるが、同じ式である。
とする本もあるが、同じ式である。
自由度2重調整済み決定係数
対馬(2007).SPSSで学ぶ医療系データ解析 p223
によると、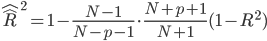 というのがあるらしいが、何をしているのか訳が分からないよ。
というのがあるらしいが、何をしているのか訳が分からないよ。
関連
参考図書
- 対馬(2007).SPSSで学ぶ医療系データ解析 p222-224
- 涌井(2001).図解でわかる多変量解析 : データの山から本質を見抜く科学的分析ツール p237-242
![[PukiWiki] [PukiWiki]](image/stat_logo.jpg)